简介
本文用Java实例介绍查找算法及其原理。
本内容也是Java后端面试常见的问题。
查找定义
查找定义:根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素(或记录)。
查找算法分类
- 静态查找和动态查找。(静态或者动态都是针对查找表而言的。)
- 静态:先给一堆值,然后在一堆值中查找元素。
- 动态:查找的过程中,有删除和插入操作。
- 无序查找和有序查找。
- 无序查找:被查找数列有序无序均可;
- 有序查找:被查找数列必须为有序数列。
顺序查找
顺序查找的基本思想
顺序查找也称为线形查找,属于无序查找算法。从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功;若扫描结束仍没有找到关键字等于k的结点,表示查找失败。
顺序查找适合于存储结构为顺序存储或链接存储的线性表。
顺序查找的复杂度
查找成功时的平均查找长度为:(假设每个数据元素的概率相等) ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;
当查找不成功时,需要n+1次比较,时间复杂度为O(n);
所以,顺序查找的时间复杂度为O(n)。
代码
/** 根据顺序查找的算法,返回在nums数组中key的index
* 直接在数组中遍历即可
* @param nums
* @param key
* @return 如果没有找到,返回-1
*/
public static int sequenceSearch(int[] nums,int key){
for(int i=0;i<nums.length;i++){
int now=nums[i];
if(now==key){
return i;
}
}
return -1;
}
二分查找
二分查找的基本思想
也称为是折半查找,属于有序查找算法。用给定值k先与中间结点的关键字比较,中间结点把线形表分成两个子表,若相等则查找成功;若不相等,再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表,这样递归进行,直到查找到或查找结束发现表中没有这样的结点。
元素必须是有序的,如果是无序的则要先进行排序操作。
注:折半查找的前提条件是需要有序表顺序存储,对于静态查找表,一次排序后不再变化,折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说,维护有序的排序会带来不小的工作量,那就不建议使用。
二分查找的复杂度
最坏情况下,关键词比较次数为log2 (n+1),且期望时间复杂度为O(log2 n)
ASL=log2 (n+1) -1
注意:在数组中排序后,再插入新值,要将新值后面的所有位后移一位,要O(n)时间
代码
/** 用二分查找在nums数组中查找key的index
* 先用快排对数组进行排序,然后设定begin=0,end=length-1
* mid=(begin+end)/2,查找mid的值与key的大小
* 如果相同,返回index
* 如果mid<key,那么begin=mid+1,如果mid>key,那么end=mid-1
* 然后循环,直到end<begin,返回-1
* @param nums
* @param key
* @return 如果数组中没有这个key,返回-1
*/
public static int binarySearch(int[] nums,int key){
int length=nums.length;
QuickSort.quickSort(nums, 0, length-1);
//begin=0,end=length-1
int begin=0;
int end=length-1;
//循环,直到end<begin,返回-1
while(begin<=end){
int mid=(begin+end)/2;
int now=nums[mid];
if(now==key){
//如果相同,返回index
return mid;
}
if(now<key){
//如果mid<key,那么begin=mid+1
begin=mid+1;
}
if(now>key){
//如果mid>key,那么end=mid-1
end=mid-1;
}
}
return -1;
}
插值查找
插值查找的基本思想
在介绍插值查找之前,首先考虑一个新问题,为什么上述算法一定要是折半,而不是折四分之一或者折更多呢?
打个比方,在英文字典里面查“apple”,你下意识翻开字典是翻前面的书页还是后面的书页呢?如果再让你查“zoo”,你又怎么查?很显然,这里你绝对不会是从中间开始查起,而是有一定目的的往前或往后翻。
同样的,比如要在取值范围1 ~ 10000 之间 100 个元素从小到大均匀分布的数组中查找5, 我们自然会考虑从数组下标较小的开始查找。
经过以上分析,折半查找这种查找方式,不是自适应的(也就是说是傻瓜式的)。二分查找中查找点计算如下:
mid=(low+high)/2, 即mid=low+1/2*(high-low);
通过类比,我们可以将查找的点改进为如下:
mid=low+(key-a[low])/(a[high]-a[low])*(high-low), //key:要查找的值
也就是将上述的比例参数1/2改进为自适应的,根据关键字在整个有序表中所处的位置,让mid值的变化更靠近关键字key,这样也就间接地减少了比较次数。
基本思想:基于二分查找算法,将查找点的选择改进为自适应选择,可以提高查找效率。当然,差值查找也属于有序查找。
注:对于表长较大,而关键字分布又比较均匀的查找表来说,插值查找算法的平均性能比折半查找要好的多。反之,数组中如果分布非常不均匀,那么插值查找未必是很合适的选择。
插值查找的复杂度
查找成功或者失败的时间复杂度均为O(log2 (log2 n))。
代码
与二分查找基本一样,就mid的计算方式不一样
mid=begin+(key-a[begin])/(a[end]-a[begin])*(end-begin)
/** 用插值查找查找在nums数组中查找key的index
* 先用快排对数组进行排序,然后设定begin=0,end=length-1
* mid=begin+(key-nums[begin])/(nums[end]-nums[begin])*(end-begin),查找mid的值与key的大小
* 如果相同,返回index
* 如果mid<key,那么begin=mid+1,如果mid>key,那么end=mid-1
* 然后循环,直到end<begin,返回-1
* @param nums
* @param key
* @return 如果数组中没有这个key,返回-1
*/
public static int insertionSearch(int[] nums,int key){
int length=nums.length;
QuickSort.quickSort(nums, 0, length-1);
//begin=0,end=length-1
int begin=0;
int end=length-1;
//循环,直到end<begin,返回-1
while(begin<=end){
int mid=begin+(key-nums[begin])/(nums[end]-nums[begin])*(end-begin);
int now=nums[mid];
if(now==key){
//如果相同,返回index
return mid;
}
if(now<key){
//如果mid<key,那么begin=mid+1
begin=mid+1;
}
if(now>key){
//如果mid>key,那么end=mid-1
end=mid-1;
}
}
return -1;
}
斐波那契查找
斐波那契查找的复杂度
复杂度分析:最坏情况下,时间复杂度为O(log2 n),且其期望复杂度也为O(log2 n)。
斐波那契查找的基本思想
在介绍斐波那契查找算法之前,我们先介绍一下很它紧密相连并且大家都熟知的一个概念——黄金分割。
黄金比例又称黄金分割,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值约为1:0.618或1.618:1。
0.618被公认为最具有审美意义的比例数字,这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域,而且在管理、工程设计等方面也有着不可忽视的作用。因此被称为黄金分割。
大家记不记得斐波那契数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….(从第三个数开始,后边每一个数都是前两个数的和)。然后我们会发现,随着斐波那契数列的递增,前后两个数的比值会越来越接近0.618,利用这个特性,我们就可以将黄金比例运用到查找技术中。
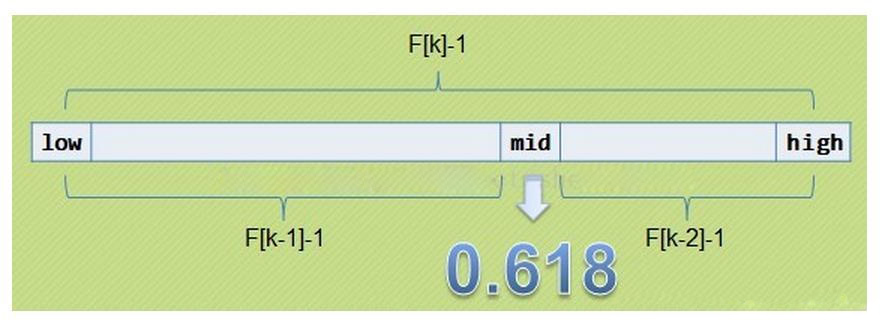
基本思想:也是二分查找的一种提升算法,通过运用黄金比例的概念在数列中选择查找点进行查找,提高查找效率。同样地,斐波那契查找也属于一种有序查找算法。
斐波那契查找与折半查找很相似,他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1,及n=F(k)-1;
开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种
1)相等,mid位置的元素即为所求
2)>,low=mid+1,k-=2;
说明:low=mid+1说明待查找的元素在[mid+1,high]范围内,k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个,所以可以递归的应用斐波那契查找。
3)<,high=mid-1,k-=1。
说明:low=mid+1说明待查找的元素在[low,mid-1]范围内,k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个,所以可以递归 的应用斐波那契查找。
为什么n=F(k)-1, 表中记录的个数为某个斐波那契数小1。
是为了格式上的统一,以方便递归或者循环程序的编写。表中的数据是F(k)-1个,使用mid值进行分割又用掉一个,那么剩下F(k)-2个。正好分给两个子序列,每个子序列的个数分别是F(k-1)-1与F(k-2)-1个,格式上与之前是统一的。不然的话,每个子序列的元素个数有可能是F(k-1),F(k-1)-1,F(k-2),F(k-2)-1个,写程序会非常麻烦。
注意:斐波那契数列 F(k)=F(k-1)+F(k-2)
F(k)-1-1=F(k-1)-1+F(k-2)-1
代码
/** 用斐波那契查找在nums数组中查找key的index
* 先用快排对数组进行排序,原先数组长度为orginalLength
* 然后建立斐波那契数列,用list不断加入,直到>orginalLength,
* 斐波那契数列的最后一位F(k),newLength=F(k)-1>=orginalLength
* 将原来排序后的数组加入长度为newLength的数组中, 多出来空位的用最后一位填满
* 然后设定begin=0,end=newLength-1,k=上面对应的k
* mid=begin+F(k-1)-1,查找mid的值与key的大小
* 如果相同,返回index,如果index>=orginalLength,返回orginalLength-1
* 如果mid<key,那么begin=mid+1,k=k-2如果mid>key,那么end=mid-1,k=k-1
* 然后循环,直到end<begin,返回-1
* @param nums
* @param key
* @return 如果数组中没有这个key,返回-1
*/
public static int fibonacciSearch(int[] nums,int key){
int orginalLength=nums.length;
QuickSort.quickSort(nums, 0, orginalLength-1);
//然后建立斐波那契数列,用list不断加入,直到>orginalLength
List<Integer> fiboList=new ArrayList<>();
fiboList.add(0);
fiboList.add(1);
int i=2;
while(true){
Integer now=fiboList.get(i-2)+fiboList.get(i-1);
fiboList.add(now);
i++;
if(now>orginalLength){
break;
}
}
//斐波那契数列的最后一位F(k),newLength=F(k)-1>=orginalLength
int k=fiboList.size()-1;
int newLength=fiboList.get(k)-1;
//将原来排序后的数组加入长度为newLength的数组中, 多出来空位的用最后一位填满
int[] newNums=new int[newLength];
for(i=0;i<newLength;i++){
if(i<orginalLength){
newNums[i]=nums[i];
}
else{
newNums[i]=nums[orginalLength-1];
}
}
//begin=0,end=newLength-1,k=上面对应的k
int begin=0;
int end=newLength-1;
//循环,直到end<begin,返回-1
while(begin<=end){
int mid=begin+fiboList.get(k-1)-1;
int now=nums[mid];
if(now==key){
//如果相同,返回index,如果index>=orginalLength,返回orginalLength-1
if(mid>=orginalLength){
return orginalLength-1;
}
return mid;
}
if(now<key){
//如果mid<key,那么begin=mid+1,k=k-2
begin=mid+1;
k=k-2;
}
if(now>key){
//如果mid>key,那么end=mid-1,k=k-1
end=mid-1;
k=k-1;
}
}
return -1;
}

请先 !